Python/알고리즘 문제 풀이
[코테] 소수 찾기
마이구미+
2023. 5. 18. 14:04

<로직 고민>
- n을 1부터 n까지 돌리고 그 안에서 또 1부터 n까지 돌려서 num % num2 == 0 이면 count를 올리고 안쪽 for문이 다 돌았을 때 count가 2이면 answer 값을 1 올리면 되겠다
- 가 제일 먼저 든 생각
- 그대로 했더니
def solution(n):
answer, count = 0, 1
for num in range(1, n+1):
for num2 in range(1, n+1):
if num % num2 == 0:
count += 1
else:
pass
if count == 2:
answer += 1
count = 0
return answer
print(solution(10)) # 3
print(solution(5)) # 3- 문제를 발견하셨나요?
- 어처구니가 없게도 count를 1부터 시작함ㅋㅋㅋ단순 오타임..!!!
def solution(n):
answer, count = 0, 0
for num in range(1, n+1):
for num2 in range(1, n+1):
if num % num2 == 0:
count += 1
else:
pass
if count == 2:
answer += 1
count = 0
return answer
print(solution(10)) # 0
print(solution(5)) # 0- 다시 0으로 초기 값을 잘 설정했는데..읭? 0이라니....
def solution(n):
answer, count = 0, 0
for num in range(1, n+1):
for num2 in range(1, n+1):
if num % num2 == 0:
count += 1
print(num, num2)
else:
pass
print("카운트", count)
if count == 2:
answer += 1
count = 0
return answer
print(solution(10))
# 1 1
# 카운트 1
# 2 1
# 2 2
# 카운트 3
# 3 1
# 3 3
# 카운트 5
# 4 1
# 4 2
# 4 4
# 카운트 8
# 5 1
# 5 5
# 카운트 10
# 6 1
# 6 2
# 6 3
# 6 6
# 카운트 14
# 7 1
# 7 7
# 카운트 16
# 8 1
# 8 2
# 8 4
# 8 8
# 카운트 20
# 9 1
# 9 3
# 9 9
# 카운트 23
# 10 1
# 10 2
# 10 5
# 10 10
# 카운트 27- answer 값을 올린 후에 count 초기화가 잘 안 되고 있었다
def solution(n):
answer, count = 0, 0
for num in range(1, n+1):
for num2 in range(1, n+1):
if num % num2 == 0:
count += 1
else:
pass
if count == 2:
answer += 1
count = 0
return answer
print(solution(10)) # 4
print(solution(5)) # 3- count 위치를 앞으로 땡겨주니 정답이 잘 나온다
- 근데 팀원분이 이런 문제는 시간복잡도에 따라 점수가 갈린다고 하셔서 줄일 수 있는 방법을 찾아봤는데
- 일단 소수 판별할 때 나누는 값인 num2를 n+1만큼 돌려줄 필요가 없다 num+1만큼만 돌려주면 된다
- 근데 또 찾아보니까 다 돌릴 필요도 없고 num의 제곱근을 찾아서 제곱근보다 작은 수 중에 0으로 나누어 떨어지는 값이 없으면 소수인 거라고 할 수 있다고 한다
- 그리고 1은 이미 모든 수로 나눠지니까 1을 나누는 수와 나눠지는 수로 둘 필요도 없다고 한다
- 아 그리고 제한 조건을 보니 이미 n은 2 이상 1000000 이하의 자연수라고 하네
import math
def solution(n):
answer, count = 0, 0
for num in range(2, n+1):
for num2 in range(2, int(math.sqrt(num))+1):
if num % num2 == 0:
count += 1
if count == 0:
answer += 1
count = 0
return answer
print(solution(10)) # 4
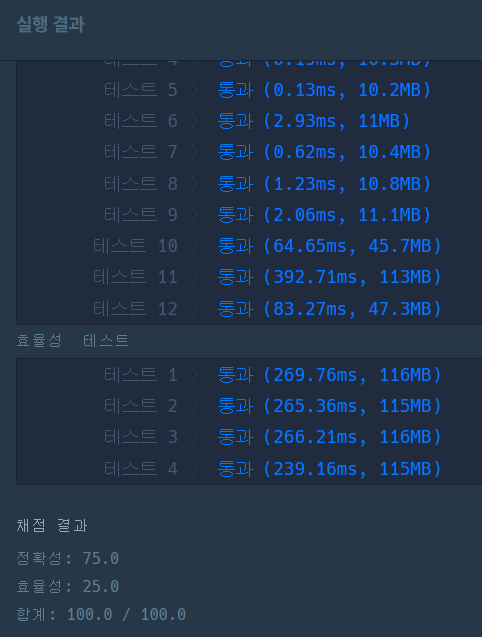
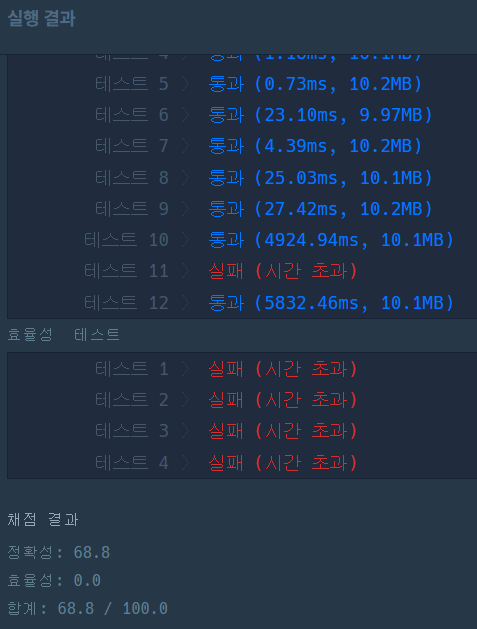
print(solution(5)) # 3- 그래서 이런 식으로 바꿔줬는데 프로그래머스에 정답을 채점하려고 하니 테스트 11에서 시간초과가 나온다
- 역시 for문이 2개 있어서 그런가..
- 소수 판별하는 함수와 카운팅하는 함수로 나눠야겠다는 생각이 들었다
- 검색하다가 에라토스테네스의 체라는 걸 알게 됐는데 어떻게 활용해야 할지 모르겠어서 일단 제껴둠..
- 함수를 나눠도 어쨌든 for문은 2번 돌아가는데 왜인지 함수를 둘로 나누니까 테스트를 통과했다
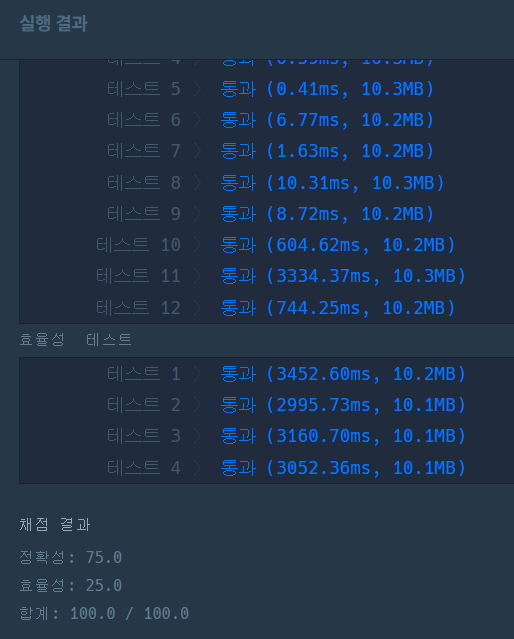
- 시간이 좀 걸리긴 했지만 그래도 시간초과는 하지 않아서 테스트가 통과됐다..ㅎㅎ
<완성된 코드>
import math
def is_prime_number(number):
for i in range(2, int(math.sqrt(number))+1):
if number % i == 0:
return 0
return 1
def solution(n):
answer = 0
for num in range(2, n+1):
answer += is_prime_number(num)
return answer
print(solution(10)) # 4
print(solution(5)) # 3<다른 사람 풀이>
- 천재풀이1
def solution(n):
num=set(range(2,n+1))
for i in range(2,n+1):
if i in num:
num-=set(range(2*i,n+1,i))
return len(num)- 에라토스테네스의 체는 이렇게 쓰는 거라고 한다...
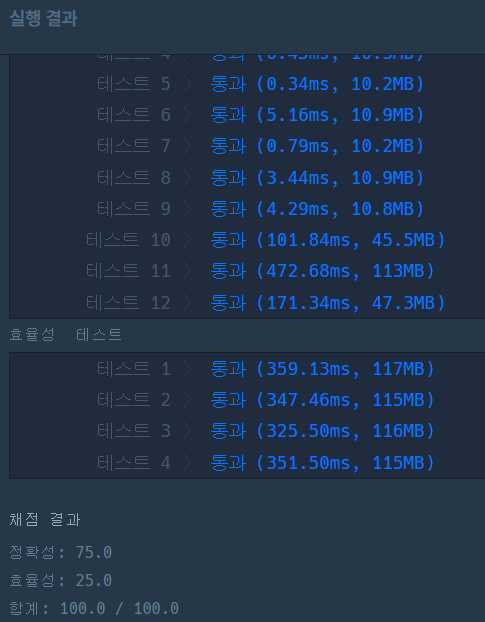
- 와 진짜 속도도 훨씬 빠르다...쩌네...
- 근데 일단 코드를 잘 모르겠어서 또 하나씩 print문을 찍어봤다
num = set(range(2, n+1))
print(num)
# {2, 3, 4, 5, 6, 7, 8, 9, 10}- 첫 번째 예시 기준으로 처음 num은 이렇게 나온다
- 그럼 num은 딕셔너리인가..? 근데 키:밸류 형식은 아닌데..흠
- 그 다음 if문은 왜 있는 것인가
- 일단 빼고 돌려봤다 답은 나온다
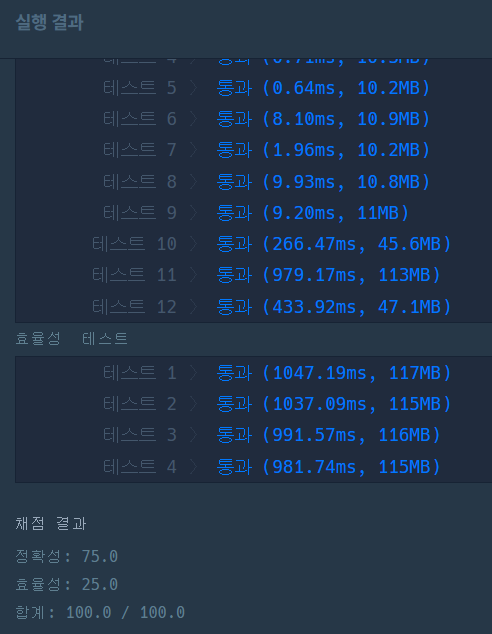
- 근데 속도가 더 떨어진다 차이가 뭐지?
def solution(n):
num = set(range(2, n+1))
print("시작 ", num)
for i in range(2, n+1):
print("for문 ", i)
if i in num:
print("if문 ", i)
num -= set(range(2*i, n+1, i))
print("배수 뺀 후 ", num)
return len(num)
print(solution(10))- 꾸질꾸질하게 print 다 찍어보기 ㅎㅎ..
시작 {2, 3, 4, 5, 6, 7, 8, 9, 10}
for문 2
if문 2
배수 뺀 후 {2, 3, 5, 7, 9}
for문 3
if문 3
배수 뺀 후 {2, 3, 5, 7}
for문 4
for문 5
if문 5
배수 뺀 후 {2, 3, 5, 7}
for문 6
for문 7
if문 7
배수 뺀 후 {2, 3, 5, 7}
for문 8
for문 9
for문 10- 시원~
- 일단 에라토스테네스의 체는 원하는 수부터 원하는 수까지의 배열을 만든 후 제일 작은 i부터 시작해서 i의 배수를 다 빼는 식으로 하는 거라고 한다
- 그래서 2부터 시작하는데 if문을 돌고 나면 2의 배수가 num에서 다 제외된다
- 그 다음 3이 num 안에 있으니 3의 배수가 num에서 다 빠지고 그렇게 쭉 for문을 다 돌면 소수만 남게 된다
- 소수만 남은 num의 길이를 구하면 그게 바로 소수의 개수..!
- 그럼 for문을 돌릴 때 num이 계속 작아지니까 끝나는 점을 max(num)+1로 하면 속도가 더 빨라지나???
num -= set(range(2*i, max(num)+1, i))- 여기만 이렇게 수정해서 돌려보니
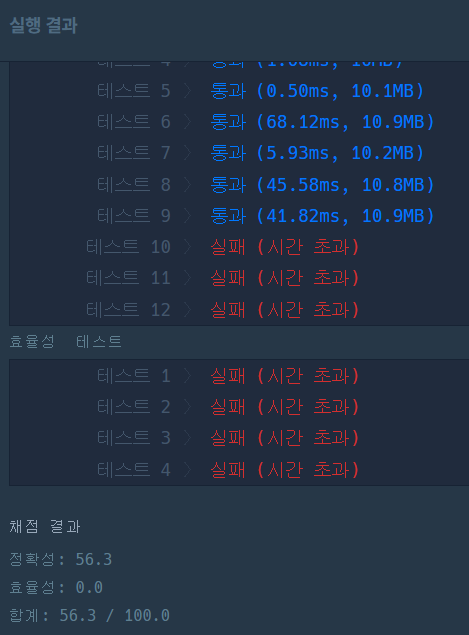
- 오...뭐지..? 안 되네~
def solution(n):
num = set(range(2, n+1))
for i in range(2, int(n**0.5)+1):
if i in num:
num -= set(range(2*i, n+1, i))
return len(num)- for문 돌릴 때 n+1이 아니라 제곱근만큼 돌리면 더 속도가 빨라진다