[코테] 최대공약수와 최소공배수

문제 링크

프로그래머스

<로직 고민/>

• 일단 최대공약수를 구해야 하는군 n과 m이 둘 다 나누어 떨어지는 숫자들로 나눠줘야 한다....소인수분해는 못 할 거 같으니...
• 근데 이러면 큰 수가 나왔을 때 시간초과 나오는 거 아냐...?? 그래도 일단 해본다

def solution(n, m):
    answer = []
    max = 1
    min = 1
    while True:
        if n % 2 == 0 and m % 2 == 0:
            n_divmod = divmod(n, 2)
            m_divmod = divmod(m, 2)
            max *= 2
        elif n % 3 == 0 and m % 3 == 0:
            n_divmod = divmod(n, 3)
            m_divmod = divmod(m, 3)
            max *= 3
        else:
            break
    min = max * n_divmod[1] * m_divmod[1]
    answer.append(max)
    answer.append(min)
    return answer

• 신택스에러가 뜨는데 좀 기다리면 시간초과도 뜬다 ㅋㅋ큐ㅠㅠ...어케 해야 되지..
• 왠지 while문이 문제인 것 같다
• 얌전하게 풀어보자,,
• 일단 최대공약수는 두 수의 공통으로 나눠지는 수니까 두 수보다는 작고 두 수 중 한 수와 같을 수도 있다
• for문을 돌리는데 두 수 중에 작은 수부터 -1씩 0이 될 때까지 돌린다
• 두 수를 i로 나눠서 공통으로 나누어 떨어지는 경우가 될 때의 i값을 answer에 붙이고 break를 건다
• 처음 나오는 그 i값이 최대공약수니까!
• 최소공배수는 두 수보다 크고 두 수 중 한 수와 같을 수도 있다
• 그리고 두 수의 곱보다 작은 수에서 최소공배수가 안 나온다면 두 수의 곱이 최소공배수가 된다
• for문을 돌리는데 두 수 중 큰 수부터 시작해서 1씩 증가하고 두 수의 곱까지 돌린다
• i를 각각 두 수로 나눠서 떨어지면 answer에 그 i값을 붙이고 break를 건다

def solution(n, m):
    answer = []
    for i in range(min(n, m), 0, -1):
        if n % i == 0 and m % i == 0:
            answer.append(i)
            break
    for i in range(max(n, m), (n * m) + 1):
        if i % n == 0 and i % m == 0:
            answer.append(i)
            break
    return answer

• 오 이렇게 하니까 예제는 풀린다
• 근데 제한사항에 두 수는 1 이상 1,000,000 이하의 자연수라고 해서... 이렇게 for문이 2개 들어가는데 심지어 1씩 증가하거나 감소하는 식이면 다른 테스트 어딘가에서 시간초과가 뜨지 않을까....?
• 시간 초과는 안 뜨더라도 어쨌든 효율성이 떨어질 것 같다
• 찾아보니까 유클리드 호제법이라는 게 있던데 이걸 활용해본다
• 글자로만 읽을 때는 이해가 잘 안 됐는데 이미지를 보니까 바로 이해했다

• 지금 푸는 문제로 따졌을 때 첫 줄을 대입하면 n=106, m=16, n % m = 10 이렇게 되는 거고
• 그 다음 줄로 가려면 n = m, n = n % m
• 그러다 m % n 값이 0이 되는 때에 n값이 두 수의 최대공약수가 된다
• 그리고 최대공배수는 (m * n) // 두 수의 최대공약수 로 구하면 된다
• 이렇게 했더니 2번째 풀이에서 실행시간이 확 줄었다..신기하군~

---

<완성된 풀이/>

- 첫 번째 풀이

def solution1(n, m):
    answer = []
    for i in range(min(n, m), 0, -1):
        if n % i == 0 and m % i == 0:
            answer.append(i)
            break
    for i in range(max(n, m), (n * m) + 1):
        if i % n == 0 and i % m == 0:
            answer.append(i)
            break
    return answer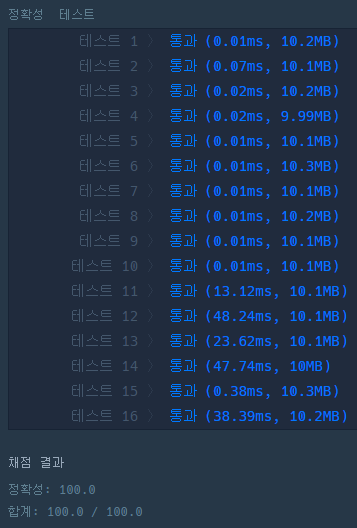

---

- 두 번째 풀이

def solution2(n, m):
    answer = []
    dn, dm = n, m
    while dm > 0:
        dn, dm = dm, dn % dm
    answer.append(dn)
    answer.append((n * m) // dn)
    return answer